10

11

12

13

14

15

a)
b)

௦)

a)

b)

a)

b)

a)

E1199 Pages: 5

PART ட்‌
Answer all questions, each carries3 marks.
Prove that in a graph G, if there is exactly one path between every pair of
vertices, then G is a tree.
Given a spanning treeof a graph, how will you find out all spanning trees ?

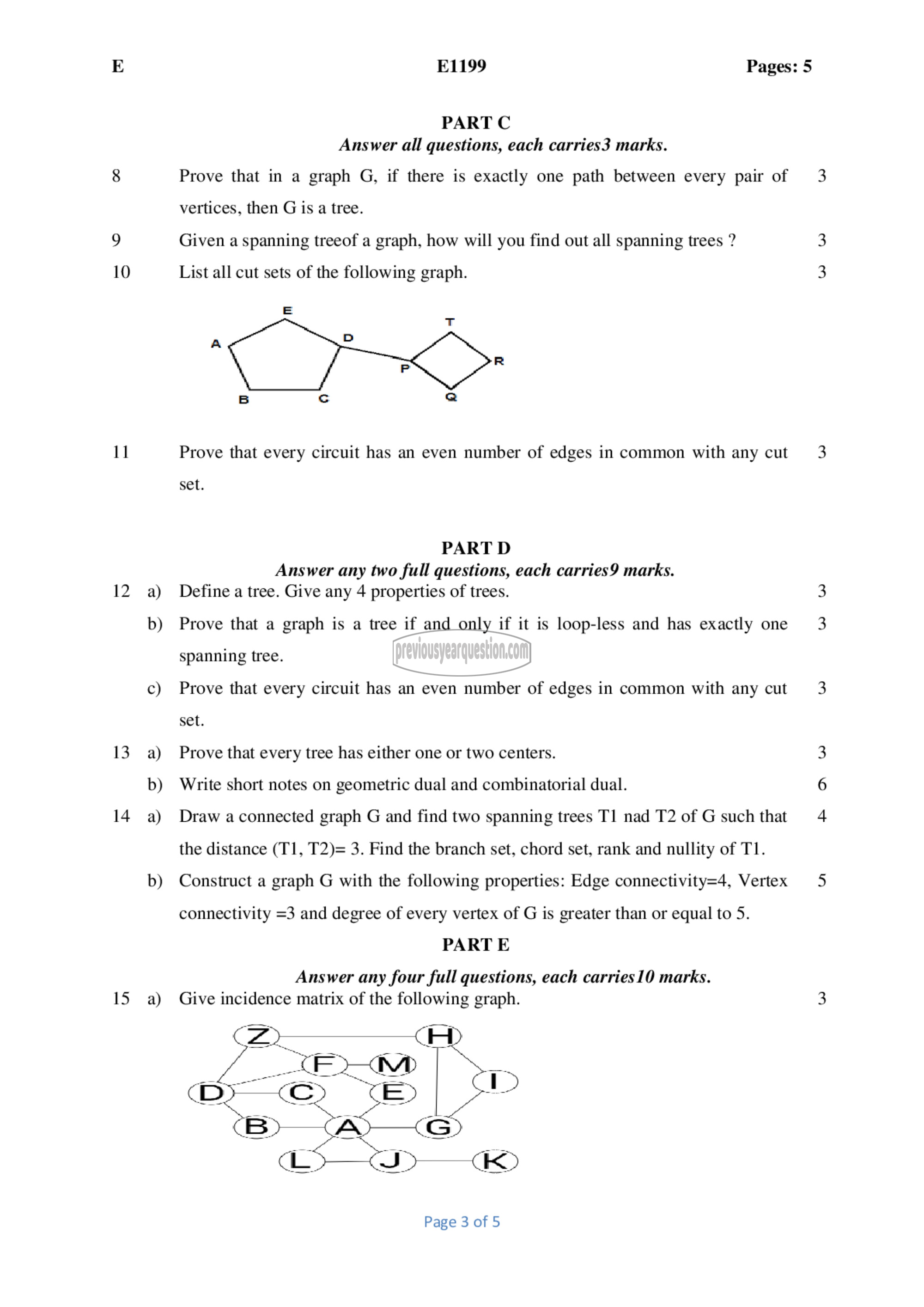
List all cut sets of the following graph.

Prove that every circuit has an even number of edges in common with any cut

set.

PART D
Answer any two full questions, each carries9 marks.
Define a tree. Give any 4 properties of trees.
Prove that a graph is a tree if and only if it is loop-less and has exactly one
spanning tree.
Prove that every circuit has an even number of edges in common with any cut
set.
Prove that every tree has either one or two centers.
Write short notes on geometric dual and combinatorial dual.
Draw ೩ connected graph G and find two spanning trees 11 nad T2 of G such that
the distance (T1, T2)= 3. Find the branch set, chord set, rank and nullity of T1.
Construct a graph G with the following properties: Edge connectivity=4, Vertex
connectivity =3 and degree of every vertex of G is greater than or equal to 5.
PARTE
Answer any four full questions, each carries 10 marks.
Give incidence matrix of the following graph.

1)

कद) कट)

Page 3 of 5