b)
0)

a)

b)

0)

೩)

0)

0)

E1199 Pages: 5

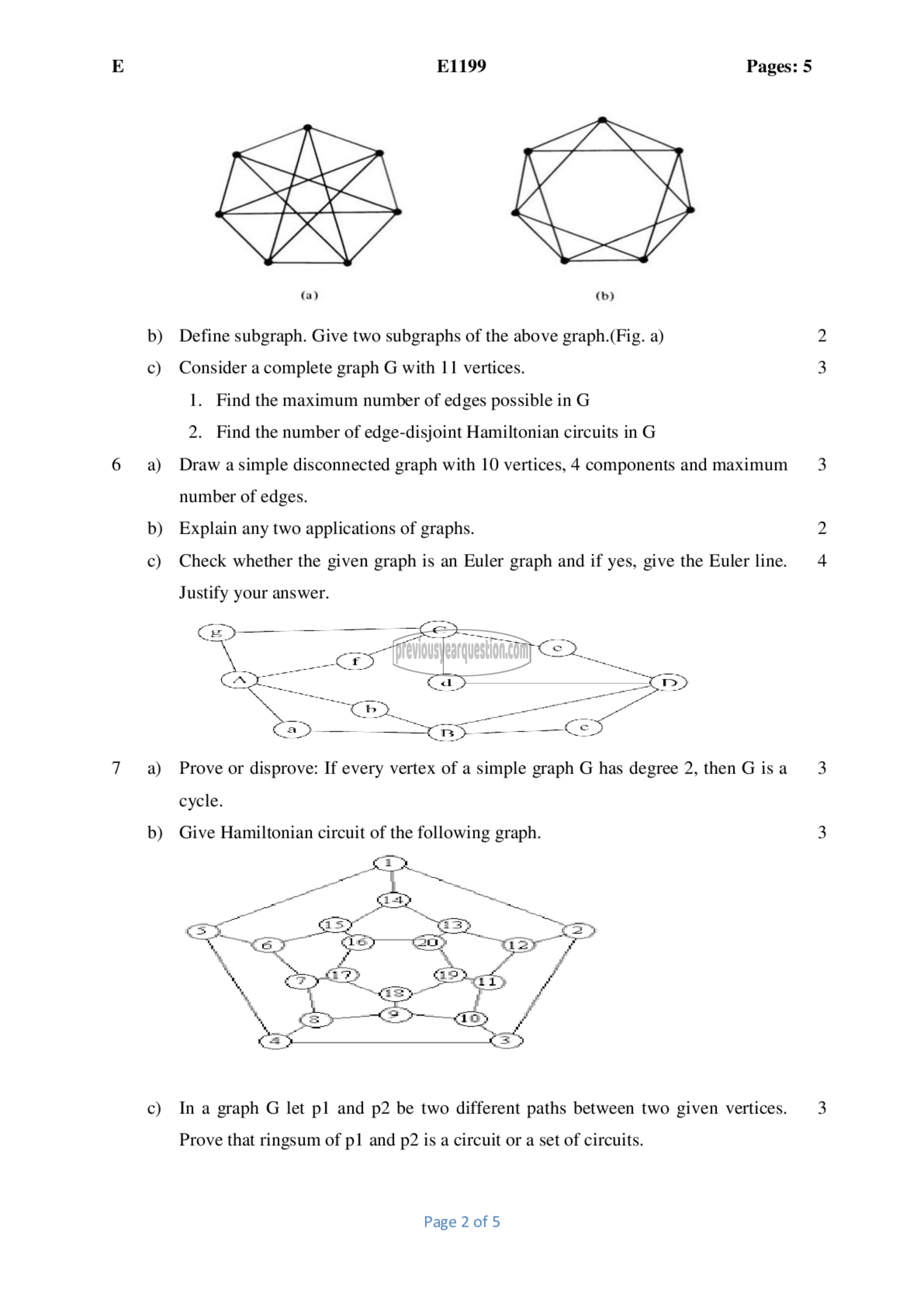
(a) (b)

Define subgraph. Give two subgraphs of the above graph.(Fig. a)
Consider a complete graph G with 11 vertices.
1. Find the maximum number of edges possible in G
2. Find the number of edge-disjoint Hamiltonian circuits in G
Draw ೩ simple disconnected graph with 10 vertices, 4 components and maximum
number of edges.
Explain any two applications of graphs.
Check whether the given graph is an Euler graph and if yes, give the Euler line.

Justify your answer.

Prove or disprove: If every vertex of a simple graph G has degree 2, then G is a
cycle.

Give Hamiltonian circuit of the following graph.

In a graph G let pl and ‏2م‎ be two different paths between two given vertices.

Prove that ringsum of ‏1م‎ and p2 is a circuit or a set of circuits.

Page 2 of 5