00000CS309121902

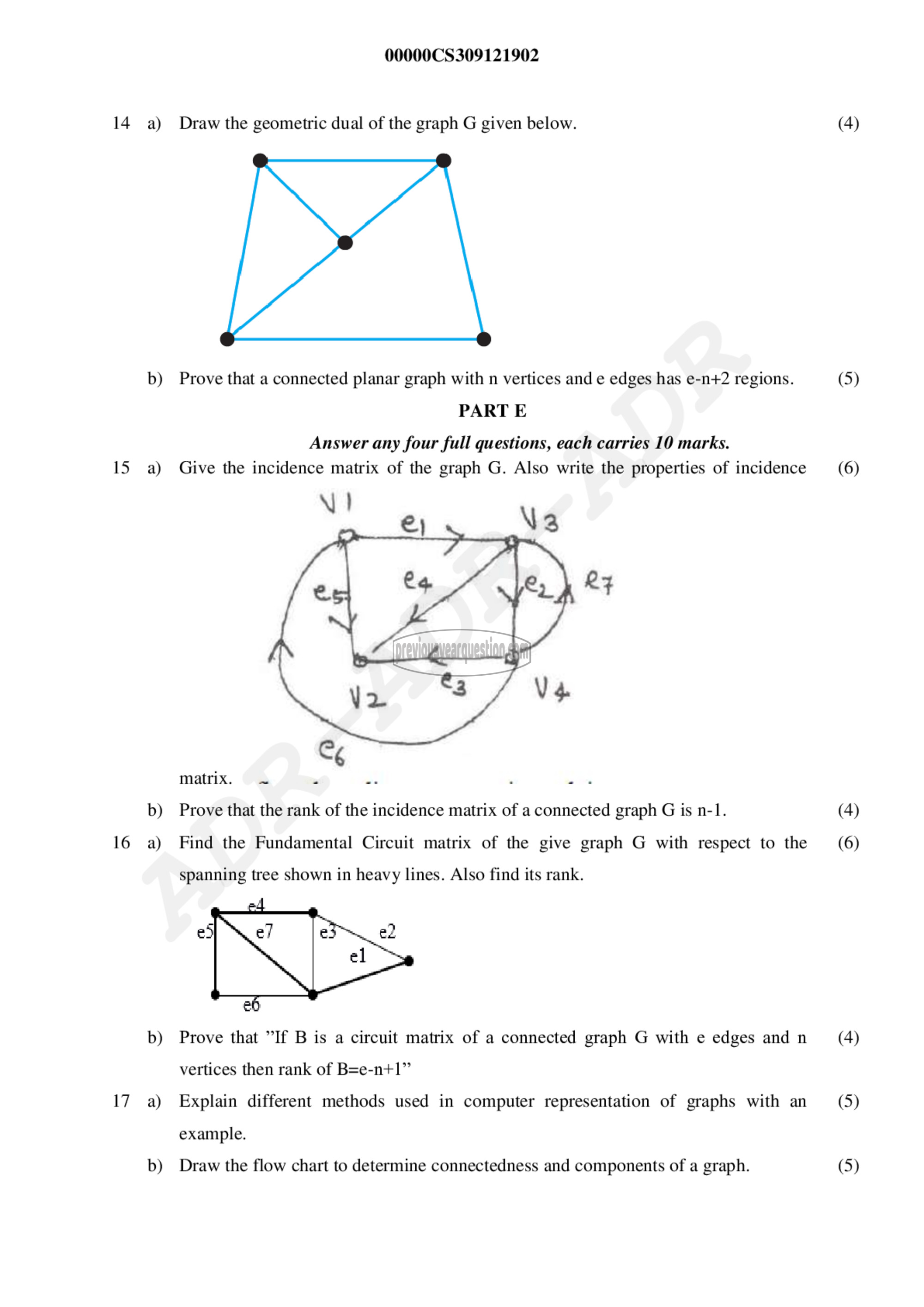
14 a) Draw the geometric dual of the graph G given below. (4)
b) Prove that a connected planar graph with n vertices and e edges has e-n+2 regions. (5)
PART E

Answer any four full questions, each carries 10 marks.
15 a) Give the incidence matrix of the graph ೮. Also write the properties of incidence (6)

099
622 Va

matrix. ~ ∙ −⋅ ⋅ ∙⋅
b) Prove that the rank of the incidence matrix of a connected graph G is n-1. (4)
16 a) Find the Fundamental Circuit matrix of the give graph G with respect to the (6)
spanning tree shown in heavy lines. Also find its rank.
⇁⋅
65 நடு இ 82
el

€
0) Prove that गा B is a circuit matrix of a connected graph © with ೮ edges andn (4)
vertices then rank of B=e-n+1”
17 a) Explain different methods used in computer representation of graphs with an (5)
example.

b) Draw the flow chart to determine connectedness and components of a graph. (5)