E

E192047 Pages:4

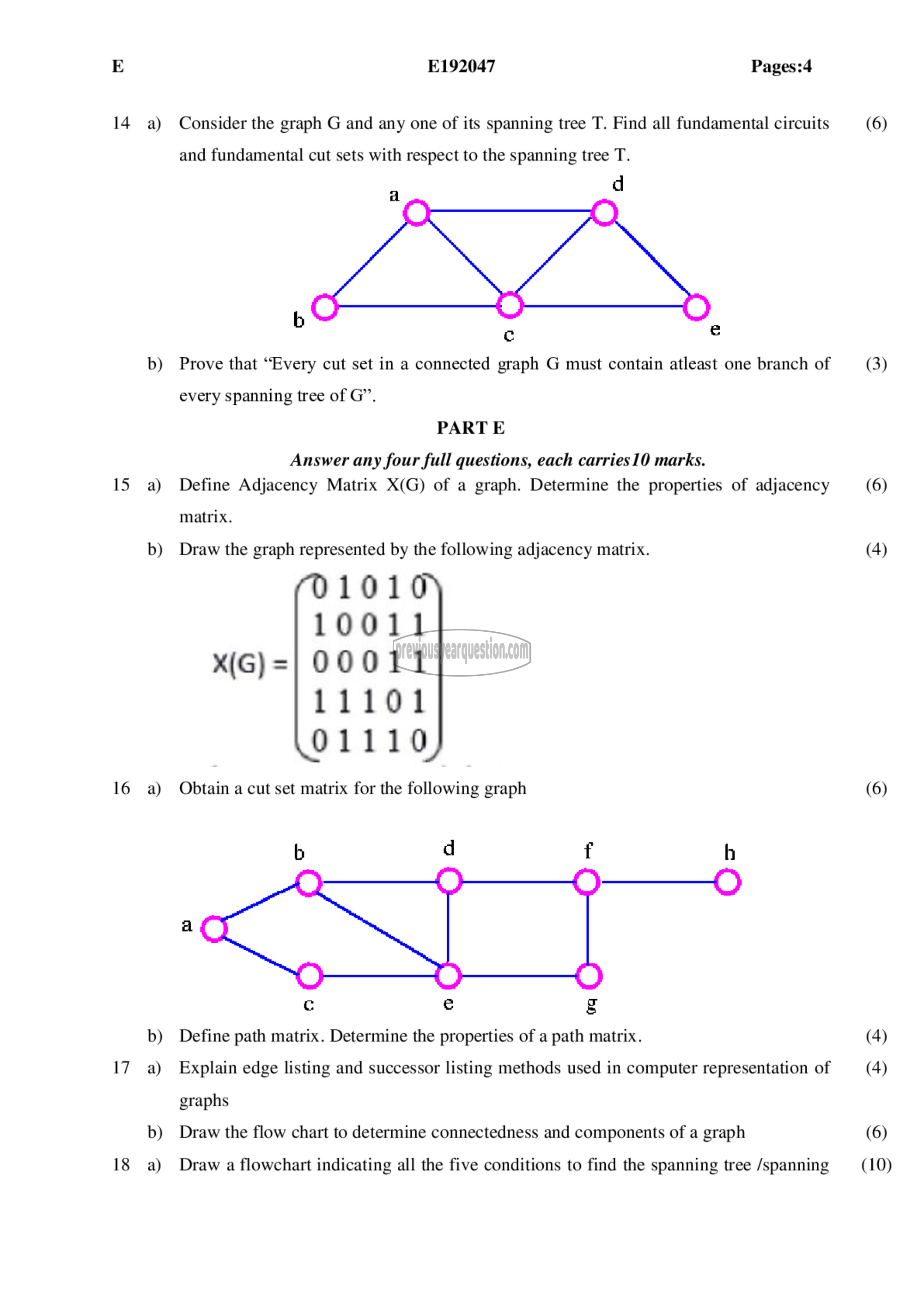
14 a) Consider the graph © and any one of its spanning tree T. Find all fundamental circuits

15

16

17

18

b)

a)

b)

a)

b)
a)

b)
a)

and fundamental cut sets with respect to the spanning tree T.

d

a

b

c 8
Prove that “Every cut set in a connected graph G must contain atleast one branch of
every spanning tree of (7,
PARTE
Answer any four full questions, each carries10 marks.
Define Adjacency Matrix X(G) of a graph. Determine the properties of adjacency
matrix.

Draw the graph represented by the following adjacency matrix.

2
10011
x(G)=| 00011
11101
01110

Obtain a cut set matrix for the following graph

b d f h
௦ 3 g

Define path matrix. Determine the properties of a path matrix.

Explain edge listing and successor listing methods used in computer representation of
graphs

Draw the flow chart to determine connectedness and components of a graph

Draw a flowchart indicating all the five conditions to find the spanning tree /spanning

(6)

(3)

(6)

(4)

(6)

(4)
(4)

(6)
(10)