O2OMINMA TANS OL

16 a) Assume shar Xfi} 15 a random process defined as follows: X(t} ~ A cos (2-0)
where A is a zero-mean ೧೦೯774! mndom variable with variance of = 2 and 9 35
uniformly dismibutcd random variable over ihe imerval - < ¢ 57. A and © are

880 150111 independent. Les ihe random variable ४ be defined as ¥ ~ 7 X(o}dt

Delermine (i) The mean ory tii) ne varience or ४.
b) rth' customcrs arrive ‏اط‎ couacer in distribution wiLh rate Tor 2 per Find pmbatiiity Lhe
inl'[val benveen consecnUve

an-ivolsis (i) hun ] minu'= Kit) bchveen mjnuLc and2 minutes,

Modale =4
17 8) Use Newton- Raphson method 0 find 8 non- zcro solution of 10525 - Cos x=0 7

b) Using Lagrange’s interpolating polynomial eslimute ‏نز‎ (5) Sor the following datn; 7
a ನ ‏یہ‎ 3 4 $
y ~ 0 30 132
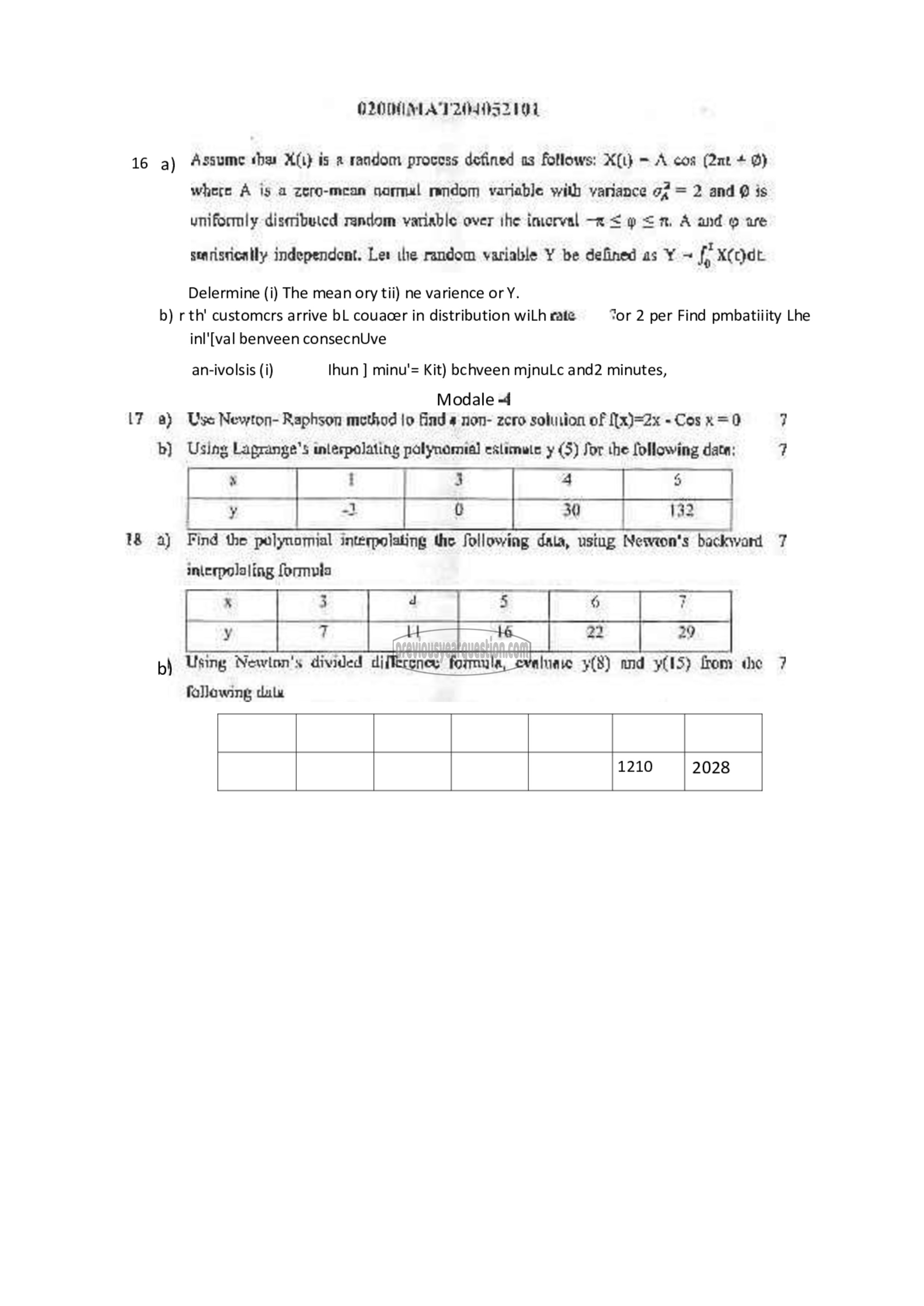
18 2) Find the polynormal interpolating the Sollowing dala, ustug Newion's backward 7

interpolaling formula
கன |

b) Using Newton's divided ധനനയ formula, evaluae ¥(8) and 012) from dhe 7
fallowing dale

_ । | | | | |

1210 2028